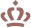Voor de liefhebber weer een nieuwe dwaling op donderdag. Uiteraard ook dit keer weer de antwoorden in het wit.
Dwaling 1: Wie is er slimmer, Jaapje of zijn moeder? Onderbouw jouw antwoord.

Dwaling 2: Staan de horizontale lijnen evenwijdig of staan ze schuin of krom?

Dwaling 3: Hoeveel zwarte stippen zie je?

Bonus dwaling:
Vijf matrozen overleven een schipbreuk en zwemmen naar een klein eiland waar ze alleen een kokosnotenboom en een aap aantreffen. De matrozen verzamelen alle kokosnoten en leggen ze in een stapel onder de boom. Uitgeput besluiten ze om pas de volgende ochtend de kokosnoten te verdelen.
Om een uur 's nachts wordt de eerste matroos wakker. Hij realiseert zich dat hij de anderen niet kan vertrouwen en besluit zijn deel alvast te nemen. Hij verdeelt de kokosnoten in vijf gelijke stapels, maar houdt daarbij een kokosnoot over. Hij geeft die kokosnoot aan de aap, verbergt zijn eigen kokosnoten (één van de vijf stapels), en plaatst de rest van de kokosnoten (de andere vier stapels) terug onder de boom.
Om twee uur 's nachts wordt de tweede matroos wakker. Zich niet bewust van het feit dat de eerste matroos zijn deel al heeft weggenomen, verdeelt ook hij de kokosnoten in vijf gelijke stapels en houdt daarbij ook een kokosnoot over, die hij aan de aap geeft. Dan verbergt hij zijn kokosnoten (één van de vijf stapels), en plaatst de rest van de kokosnoten (de andere vier stapels) terug onder de boom.
Om drie, vier en vijf uur 's nachts worden achtereenvolgens de derde, vierde en vijfde matroos wakker en voeren dezelfde handelingen uit als de eerste twee matrozen.
's Morgens, als ze opstaan, proberen ze allemaal zo onschuldig mogelijk te kijken. Geen van de matrozen maakt een opmerking over de gekrompen stapel kokosnoten, en geen van hen besluit om eerlijk te zijn en toe te geven dat hij zijn deel al genomen heeft. Ze verdelen de kokosnoten voor de zesde maal in vijf gelijke stapels en houden daarbij alweer een kokosnoot over, die ze aan de aap geven.
Uit hoeveel kokosnoten moet de oorspronkelijke stapel kokosnoten minimaal hebben bestaan?